时间

2023年6月19日

地  点

秦淮中学

主持人

吉文勇

记录人

吉文勇

参加人员

何应海，吴家美，柏寿俊，储斌，孙帮兰，严建英，邬颖杰，周国溢，

吴家林，吉文勇，郑必强

活动主题

平面向量微专题补充：巧用建系解平面向量问题

一：主备人陈述（教学目标，重难点，方法，手段，练习作业）

（一）教学内容   

巧用建系解平面向量问题

（二）教材分析

坐标法是数学中解决数形结合问题的一个重要方法．它将数学中的几何和代数巧妙地联系起来，使一部分问题的解决变得简单容易．利用坐标法时，要合理建系，根据坐标运算和性质，建立等式或代数关系解决问题．

（三）教学目标

关于平面向量补充专题，建系解平面向量问题，如果大家前面几个专题来不及讲的，这个讲义讲完就可以了！3.4.5.10.16等可以用极化恒等式去做，8题我改了一下，可以用基底法去做，14题数量积问题可以转化成投影去做又出现了一遍。16到19补充一下设三角函数求最值问题！

出题宗旨是基底法坐标法作为主打方法渗透，出现向量共起点数量积问题，联想投影或者极化恒等式。

不到之处，请大家斧正！

（四）教学思路与方法

教学过程分为问题自学展示提炼要点、探索巩固、应用知识阶段，总结提炼！

二：组员陈述（教学目标，重难点，方法，手段，练习作业）

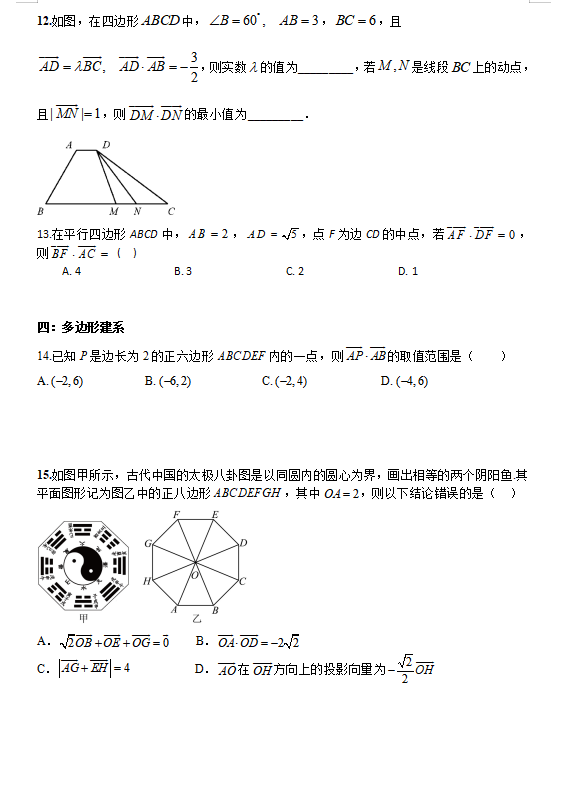
何应海老师说：坐标是向量代数化的媒介，对于某些平面向量问题，若能建立适当的平面直角坐标系，往往能很快实现

问题的转化，从而快速简捷地达成解题的目标．

吴家美老师说：常见的建系方法如下：

1．利用图形中现成的垂直关系：若图形中有明显互相垂直且相交于一点的两条直线（如矩形、直角梯

形等），可以利用这两条直线建立平面直角坐标系．

2．利用图形中的对称关系：图形中虽没有明显互相垂直交于一点的两条直线，但有一定对称关系（如：等腰三角形、等腰梯形等），可利用自身对称性建立平面直角坐标系．建立平面直角坐标系的基本原则是尽可能地使顶点在坐标轴上或在同一象限内．

．当三角形中有唯一一个特殊角（30°,45°,60°等）时，有以下两种建系方法。

60°

4．圆（或半圆、扇形）与其他图形的综合图形通常以圆心为坐标原点建立平面直角坐标系．

5．所给向量中任意两向量之间的夹角为特殊角，将所给向量平移为共起点，以该起点为坐标原点建立平面直角坐标系。

吴家林老师说：从基础入手，让学生掌握好基础知识。开展多角度研究  促进学生理解。

柏寿俊老师说：教学无盲点讲清知识逻辑，授人以渔强调计算的重要性，苦练基本功

构建知识体系，拓展思维宽度新高考反押题倾向明显，夯实基础才是王道.

严建英：

考点：常见建立坐标系方法

边长为的等边三角形   正方形        已知夹角的任意三角形         矩形

 直角梯形         平行四边形             等腰梯形             圆

三：活动小结

渗透极化恒等式的方便，由几何法到代数法，代数法到几何法，让学生有最直观的体验！